Ever wondered why rockets are essentially giant fuel tanks with tiny payloads? The answer lies in an equation penned by a self-taught Russian schoolteacher in 1897.
Konstantin Tsiolkovsky’s rocket equation isn’t just a mathematical equation; it’s the fundamental law that governs every spacecraft ever launched.
Understanding it means grasping why multi-stage rockets exist, why reaching orbit is so expensive, and what physical barriers stand between us and the stars.
Ready to decode the equation that discovered the cosmos? Let’s break down the mathematics that transformed space travel from fantasy into reality!
Who was Konstantin Tsiolkovsky?
Konstantin Eduardovich Tsiolkovsky was born in 1857 in rural Russia. As a young boy, he contracted scarlet fever, which caused significant hearing loss, and he educated himself through books and independent study.
His curiosity and determination led him to spend much of his time learning concepts in mathematics, physics, and engineering.
During a period when powered flight had yet to become reality, Tsiolkovsky was already imagining the possibilities of space travel.
His key contributions to the space exploration were:
- The Rocket Equation (1903): He derived what we now call the Tsiolkovsky Rocket Equation, laying out the fundamental relationship between a rocket’s velocity, its exhaust velocity, and its changing mass.
- Multistage Rockets: He proposed the concept of staging using multiple rocket segments to overcome the limits of single-stage designs.
- Space Colonization Ideas: Beyond engineering, he imagined space stations, orbital habitats, and even colonization of the solar system. His famous belief was that “Earth is the cradle of humanity, but one cannot live in the cradle forever
What is the Tsiolkovsky Rocket Equation?
The Tsiolkovsky Rocket Equation, also called the ideal rocket equation, is a mathematical formula that explains how rockets change speed as they burn fuel.
It was first published in 1903 by Konstantin Tsiolkovsky and remains one of the most important equations in spaceflight.
At its core, the equation is written as:
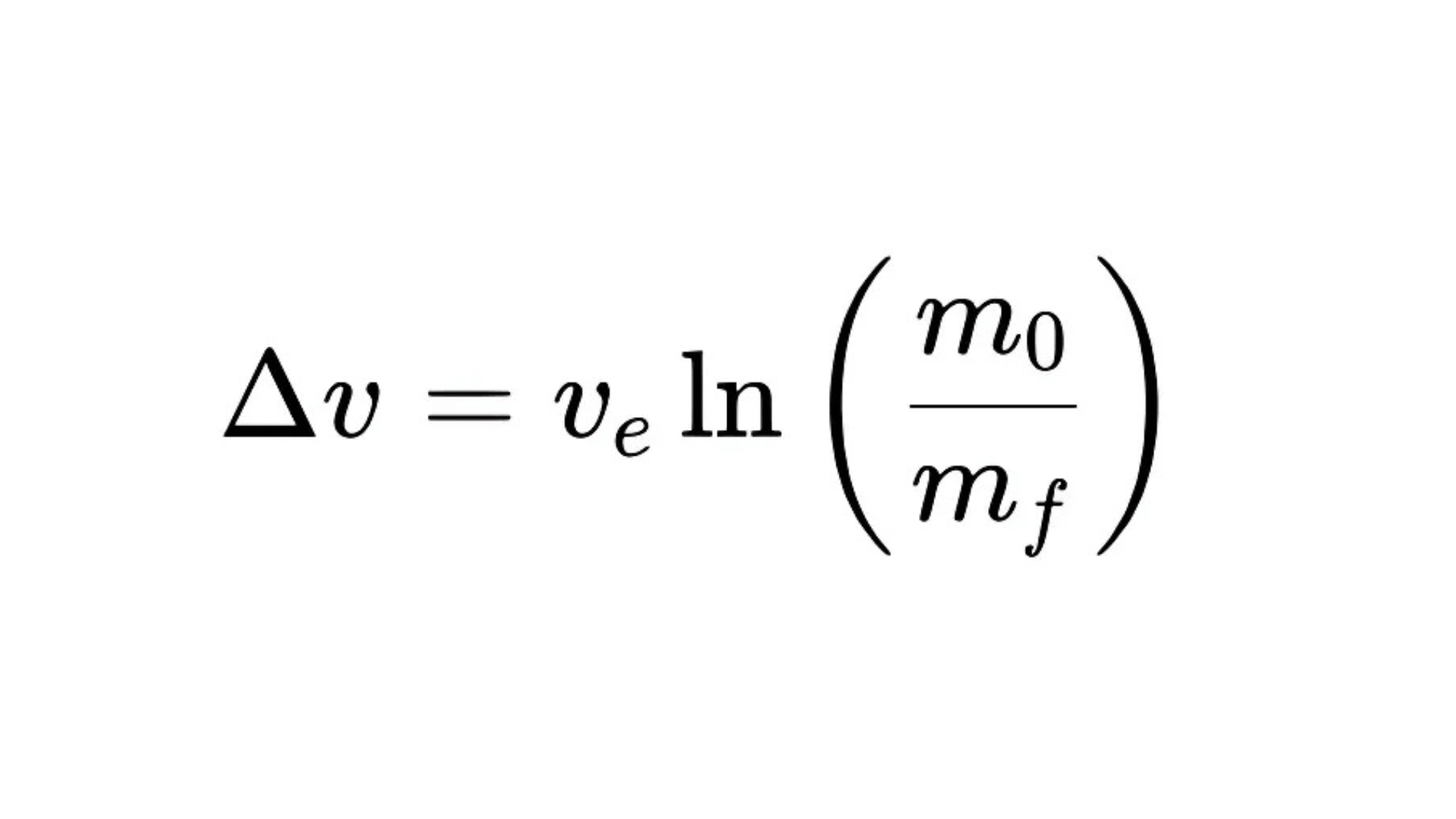
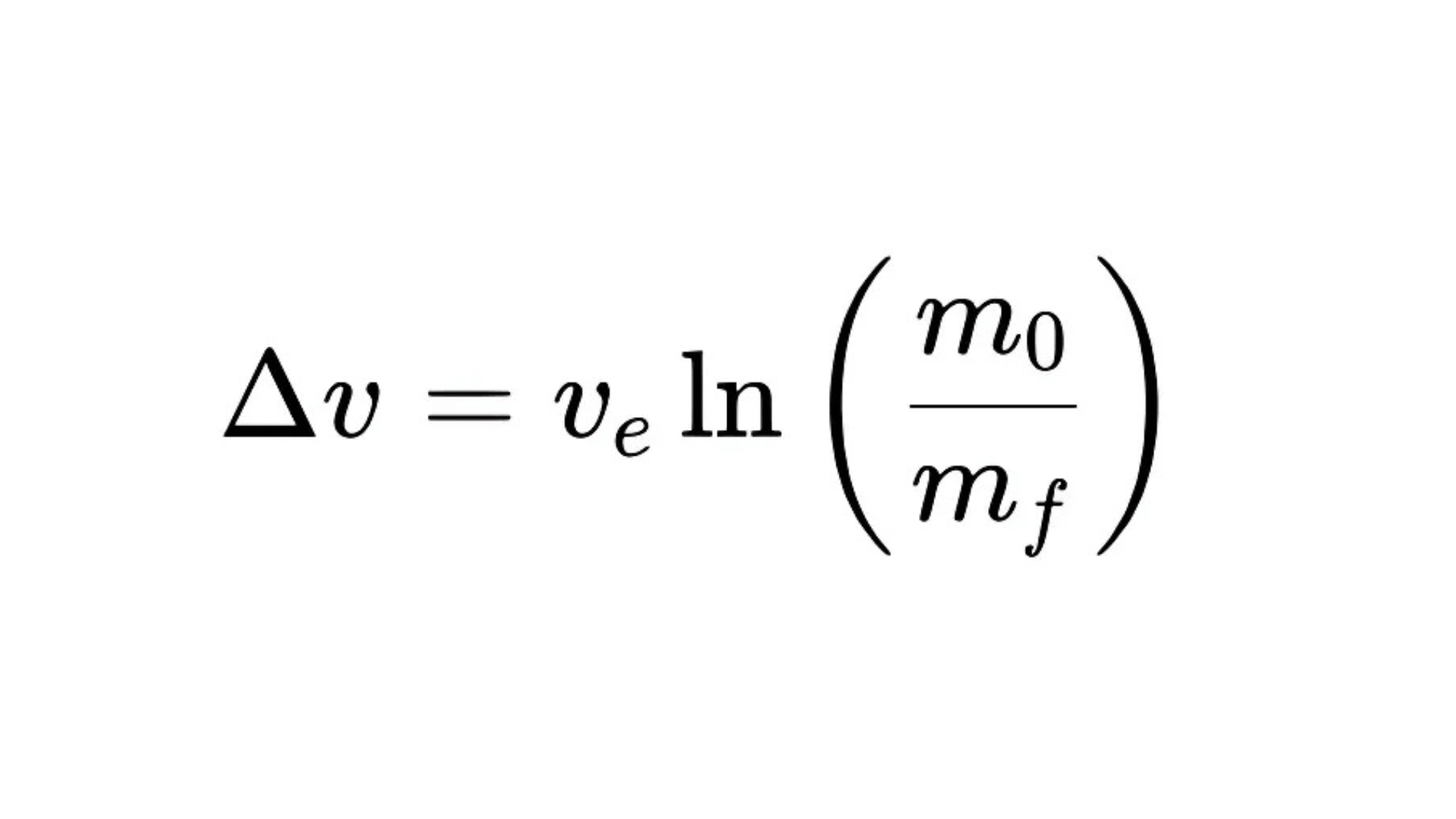
Where:
- Δv (Delta-v): The change in velocity a rocket can achieve; a critical measure in mission planning.
- ve: The effective exhaust velocity of the propellant (closely related to specific impulse).
- m0: The initial mass of the rocket (including fuel).
- mf: The final mass of the rocket (after the fuel has been burned)
Role of the Tsiolkovsky Rocket Equation in Spaceflight
This equation is far more than a piece of abstract math; it’s the foundation of modern space travel. It matters because it explains both the possibilities and the limitations of rocket propulsion.
1. Planning Space Missions
The equation allows engineers to calculate whether a mission is feasible before building anything.
By knowing the required velocity change and available propellants, they can determine the fuel mass needed, helping design realistic spacecraft and set achievable mission objectives.
2. The Mass Ratio Problem
The equation exposes an exponential relationship between fuel and velocity.
Achieving higher speeds requires disproportionately more fuel, which adds weight, demanding even more fuel. This creates a compounding problem where most of a rocket’s mass must be propellant rather than payload.
3. Why Staging is Essential
Multi-stage rockets discard empty fuel tanks during flight, dramatically improving the mass ratio.
The equation mathematically proves why this works: each stage operates more efficiently without carrying dead weight from previous stages, making otherwise impossible missions achievable with current technology.
4. Linking Theory to Reality
Tsiolkovsky’s 1897 theoretical work provided the mathematical foundation that rocket engineers still use today.
Every modern spacecraft from SpaceX’s Falcon 9 to NASA’s SLS is designed using his equation, demonstrating how pure theory became the practical blueprint for humanity’s journey into space.
Applications That Make Space Travel Possible
The Tsiolkovsky rocket equation is applied throughout every phase of space mission development:
1. Launch Vehicle Design
Engineers rely on the Tsiolkovsky equation as their primary design tool when creating launch vehicles.
By calculating the delta-v required to reach orbit, roughly 9.4 km/s from Earth’s surface, and knowing their propellant’s exhaust velocity, they work backward to determine fuel requirements.
This establishes the rocket’s mass ratio, which dictates tank sizes, structural dimensions, and payload capacity.
The equation reveals why rockets must be 85-90% fuel by mass, fundamentally shaping vehicle architecture.
2. Orbital Maneuvers
Once in space, satellites and spacecraft continuously apply the equation for mission operations.
Controllers use it to budget propellant for orbit raising, inclination changes, station-keeping against atmospheric drag, and attitude control.
Each maneuver consumes precious fuel reserves that must last the spacecraft’s entire operational lifetime, often 15-20 years for satellites. The equation allows precise calculation of remaining capabilities after each burn.
Mission success depends on accurate fuel accounting; running out of propellant means premature mission end, even if all other systems function perfectly
3. Interplanetary Missions
Deep space exploration demands multiple velocity changes throughout the trip, course corrections, gravity-assist flybys, and planetary orbit insertions.
The rocket equation helps mission planners construct detailed delta-v budgets for the entire multi-year voyage.
Engineers must balance scientific payload mass against fuel requirements, often making difficult trade-offs.
It also reveals why missions to outer planets require gravity assists; the fuel requirements for direct trajectories would be prohibitively large
4. Propulsion System Comparison
The equation provides a standardized framework for evaluating different propulsion technologies based on their specific impulse (exhaust velocity).
Chemical rockets offer high thrust but moderate efficiency, while ion drives provide exceptional exhaust velocities but minimal thrust.
By plugging various propulsion systems into the equation, engineers can determine which technology best suits specific mission profiles.
This analysis guides research investments and technology development.
The Limitations of the Tsiolkovsky Equation
While the Tsiolkovsky Rocket Equation is a cornerstone of rocket science, it’s also an idealized model. In real-world rocketry, several important factors limit its direct application:
- Assumes a Perfect Vacuum: The equation works best in empty space, but real rockets must push through atmospheric drag and air resistance during launch.
- Ignores Gravity Losses: It doesn’t account for the constant pull of gravity, which consumes a large portion of fuel before reaching orbit.
- Assumes Constant Exhaust Velocity: In practice, engine performance and exhaust velocity vary with design, propellant type, and operating conditions.
- No Structural or Engineering Limits: Real rockets carry tanks, engines, and guidance systems that reduce the ideal fuel-to-mass efficiency.
- Neglects External Influences: Orbital maneuvers, planetary gravity assists, and landing complexities aren’t captured in the equation.
Broader Impact and Legacy of the Equation
Konstantin Tsiolkovsky wasn’t just a mathematician; he was a visionary who dared to dream when space travel seemed impossible.
His famous words
“Earth is the cradle of humanity, but one cannot remain in the cradle forever,”
captured a philosophy that transcended equations, redefining that we are destined for the cosmos.
His theoretical work laid the groundwork for the Soviet space program.
Pioneers like Sergei Korolev changed Tsiolkovsky’s calculations into the rockets that launched Sputnik and carried Yuri Gagarin into history.
Today, every aerospace student learns their equation, Craters bearing his name dot the Moon and Mars, silent tributes to a man who proved that one person’s imagination, armed with mathematics and conviction, could chart humanity’s path to the stars.
Conclusion
The Tsiolkovsky rocket equation stands as a testament to the power of theoretical thinking. It uncovered a fundamental truth that still governs space exploration today.
As we push toward Moon bases and Mars colonies, Tsiolkovsky’s principles remain our guiding framework, reminding us that some truths are timeless.
Understanding this equation means understanding the very physics that will carry humanity to the stars. It’s not just history, it’s the blueprint for our future in space.
Found this helpful? Drop us a comment with questions about rocket propulsion or suggest topics you’d like us to explore next.