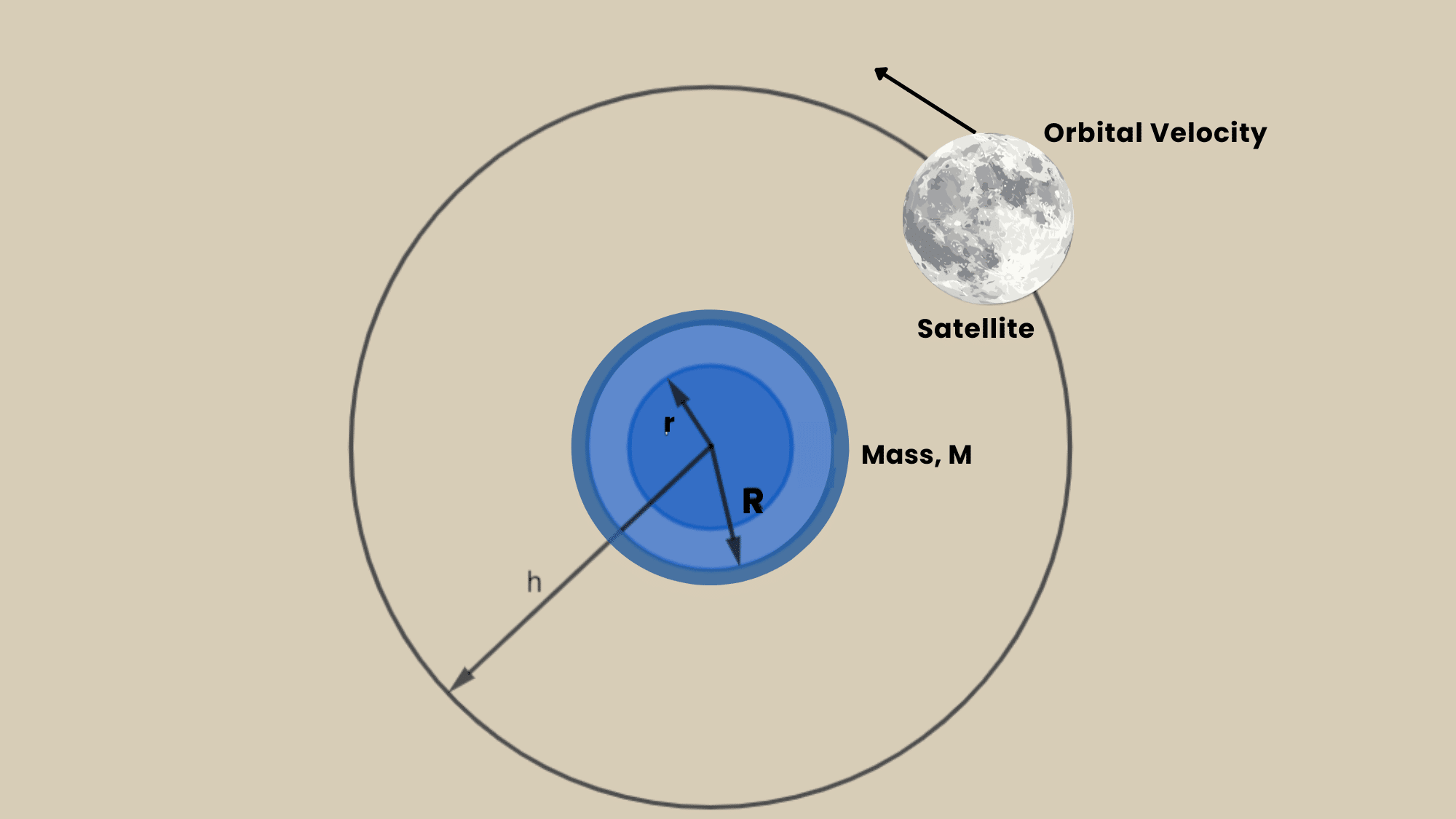
Orbital velocity and orbital speed sound like the same thing, right? After all, both describe how fast something moves around another object in space.
But physics has a sneaky way of using similar-sounding terms that mean different things. And this confusion isn’t just for students cramming for exams. Even space enthusiasts mix them up.
So what’s the real difference? Are these terms interchangeable, or is there something more to the story?
The answer might surprise anyone who’s ever looked up at satellites circling Earth or wondered how the Moon stays in its orbit. Let’s clear up this cosmic confusion.
What is Orbital Speed?
Orbital speed is straightforward. It’s how fast an object travels along its orbital path.
Think of it as the speedometer reading if a satellite had one. This speed tells us the distance covered per unit of time, nothing more.
A satellite zipping around Earth at 7.8 kilometers per second has that orbital speed, regardless of which direction it’s heading.
The formula is simple: divide the distance traveled by the time taken. No directional information needed. Just pure speed. And orbital speed stays fairly constant for circular orbits.
It’s the number that keeps satellites from falling back to Earth or drifting into space.
How Gravity Determines Orbital Velocity
Gravity is the puppet master behind orbital motion. It pulls objects toward the center, creating that perfect balance between falling and moving forward.
The stronger the gravitational pull, the faster an object must move to maintain its orbit. That’s why satellites closer to Earth zip around much quicker than those farther out.
The mass of the central body matters too. Jupiter’s massive gravitational field demands higher orbital velocities than Earth’s.
And distance plays a crucial role. Double the distance, and the required orbital velocity drops. It’s this gravitational dance that keeps everything from moons to space stations in their designated paths.
Differences Between Orbital Velocity vs. Orbital Speed
While they sound similar, orbital velocity and orbital speed have one key difference that changes everything in physics calculations.
| Aspect | Orbital Speed | Orbital Velocity |
|---|---|---|
| Definition | Rate of motion along the orbital path | Rate of motion with directional information |
| Nature | Scalar quantity | Vector quantity |
| Direction | No directional component | Includes directional component |
| Measurement | Magnitude only (e.g., 7.8 km/s) | Magnitude and direction (e.g., 7.8 km/s tangent to orbit) |
| Changes in Orbit | Remains constant in circular orbits | Changes continuously as direction changes |
| Formula Focus | Distance divided by time | Displacement divided by time |
| Use in Calculations | Simple motion problems | Complex physics and engineering calculations |
Orbital Speed Formula and Orbital Velocity Formula Breakdown
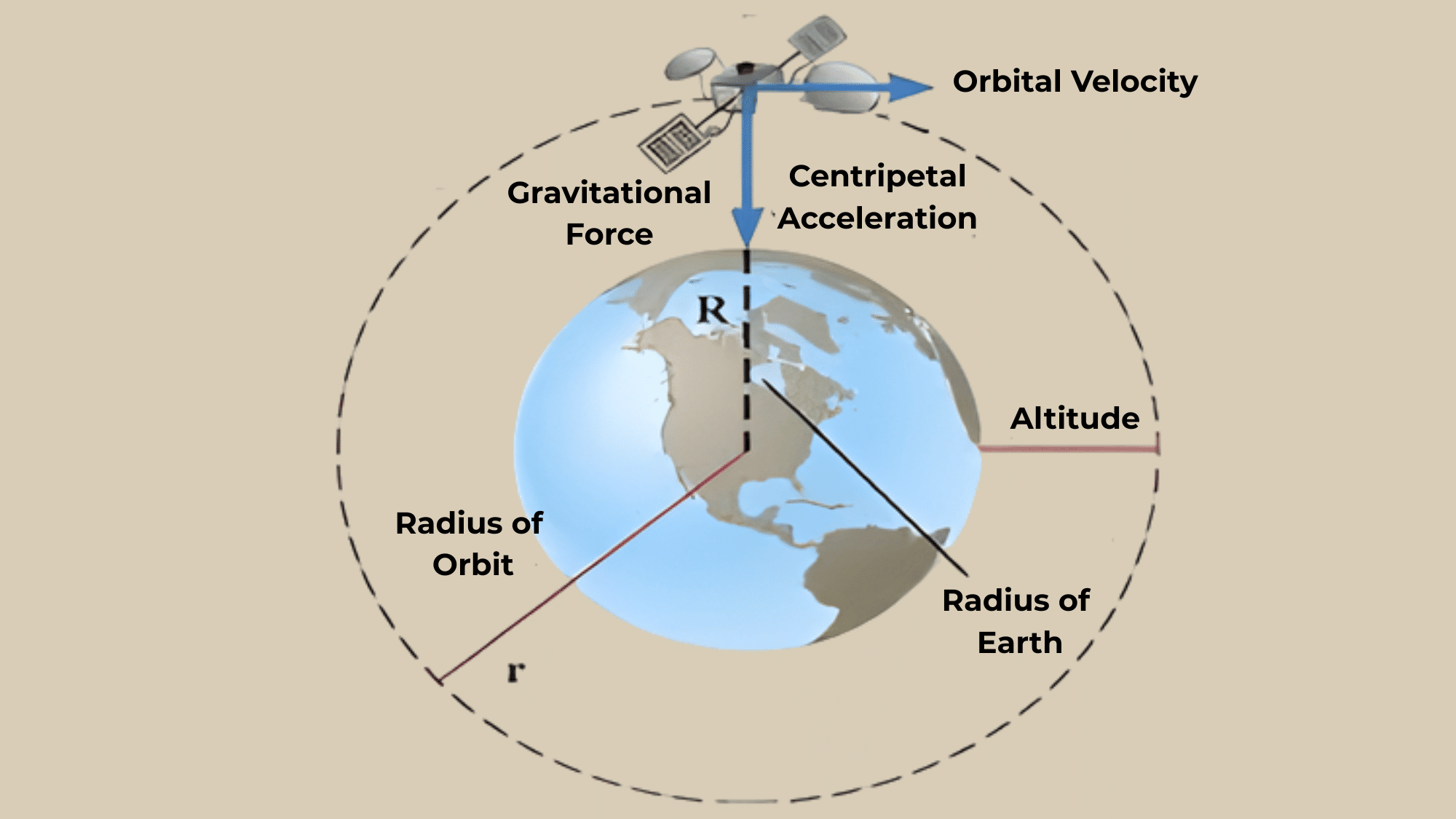

The orbital speed formula reveals the mathematical relationship between gravity, mass, and distance that keeps objects circling in stable orbits.
Formula:
v = √(GM/r)
Where:
- v= Orbital speed (meters per second)
- G = Gravitational constant (6.67430 × 10⁻¹¹ m³ kg⁻¹ s⁻²)
- M= Mass of the central body (kilograms)
- r= Orbital radius from the center (meters)
Formula Derivation:
For a satellite of mass m in orbit, gravitational force provides the centripetal force needed for circular motion. Setting these equal gives:
GMm/r² = mv²/r
Canceling m from both sides and multiplying by r:
GM/r = v²
Taking the square root of both sides:
v = √(GM/r)
Key Insights:
- Orbital speed decreases as distance increases (inverse square root relationship)
- Larger central body mass means a higher required orbital speed
- The satellite’s own mass doesn’t affect its orbital speed
Factors Affecting Orbital Speed Formula
Several factors influence how fast an object must travel to maintain a stable orbit around a celestial body or planet.
1. Mass of the Central Body: The heavier the object being orbited, the stronger its gravitational pull. Earth’s mass creates a specific gravitational field that determines how fast satellites must move. More massive planets like Jupiter require significantly higher orbital speeds.
2. Orbital Radius (Distance from Center): Distance matters enormously. Objects closer to the central body need greater speeds to resist the stronger gravitational pull. Move farther out, and the required speed decreases. The International Space Station orbits much faster than the Moon for this reason.
3. Gravitational Constant: This universal value ties everything together in orbital mechanics. It appears in every orbital speed calculation, connecting mass and distance to the speed needed. Without it, predicting satellite motion would be impossible.
4. Orbit Shape (Eccentricity): Circular orbits maintain constant speed throughout. Elliptical orbits cause speed variations; faster at the closest approach, slower at the farthest point. The more elongated the orbit, the greater these speed differences become during each revolution
Orbital Speed in Low Earth Orbit vs. Geostationary Orbit
Different orbital altitudes require vastly different speeds. Comparing low Earth orbit and geostationary orbit shows how distance dramatically affects orbital motion.
Low Earth Orbit (LEO)
Low Earth orbit sits between 160 to 2,000 kilometers above Earth’s surface. Satellites here must travel incredibly fast, around 7.8 kilometers per second or roughly 28,000 kilometers per hour.
The International Space Station operates in this zone, completing one full orbit every 90 minutes. This closeness to Earth means a stronger gravitational pull, demanding higher speeds to avoid falling back down.
Geostationary Orbit (GEO)
Geostationary orbit exists at approximately 35,786 kilometers above the equator.
Satellites here move much slower, about 3.07 kilometers per second or 11,000 kilometers per hour. But this speed perfectly matches Earth’s rotation.
The satellite appears stationary from the ground, making it ideal for communication and weather satellites. The weaker gravitational pull at this distance requires less speed to maintain orbit.
Speed Comparison
LEO satellites travel more than twice as fast as GEO satellites. Yet GEO satellites cover a larger circular path in 24 hours.
The trade-off is clear: closer orbits need higher speeds but complete revolutions quickly, while distant orbits need lower speeds but take much longer to circle Earth.
Conclusion
Understanding the distinction between orbital velocity and orbital speed matters more than semantics.
Speed gives the number, velocity adds direction, and that directional component changes everything in orbital mechanics. The formula shows how gravity and distance work together.
These aren’t just classroom concepts. Every GPS signal, weather forecast, and communication satellite depends on engineers applying these principles correctly.
Next time someone mentions orbital motion, the difference between speed and velocity won’t just be clear; it’ll reveal the physics keeping our technology floating overhead.